Здравствуйте
1. Используя свойства верных числовых неравенств, докажите, что возрастают функции
1) у = 9 + 2 х
2) у = - 8 + 4х
2. Найдите наибольшее и наименьшее значения функций
1) у = 1,5 + 6 х, где
2)
, где
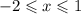
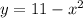
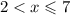
Другие вопросы по теме Алгебра
Популярные вопросы
- Предпочитай услышать все из первых рук...
1 - Впенале x ручек,а карандашей в 2 раза больше.сколько в пенале ручек...
3 - Какое кол-во теплоты выделится при полном сгорании 250 литров невти?...
3 - Вмолекулу входят 3 атома водорода , один атом фосфора и четыре...
3 - Объясните как выглядит фронтальная проекция, горизонтальная и профильная...
1 - Площадь прямоугольника 24 см кв. найдите периметр прямоугольника...
1 - Как из 1/2 - 4/17 скажите решение это дроби...
2 - Как дышит речной рак: а) атмосферным кислородом б) кислородом,...
2 - Автомобиль двигаясь со скоростью 54 км/ч проходит путь равный 5...
1 - 1703+x=1213+490 x+1547=1970+749 x: 3-18=12 5×x+80=690 x×8+120=280...
3
1. Если угловой коэффициент к положителен, линейная функция возрастает. если отрицателен, то убывает. в 1) к=2>0 ; во 2) k=4>0, значит, обе функции возрастают.
второй Используя свойства верных числовых неравенств, докажем, что возрастают функции
1) у = 9 + 2 х
Пусть х₁>х₂, у₁ = 9 + 2 х₁; у₂ = 9 + 2 х₂; тогда 2х₁>2х₂, т.к. умножали на положительное одно и то же число 2, 9+2х₁>9+2х₂, т.к. к обеим частям добалили одно и то же число 9, вывод у₁>у₂, доказано.
2) у = - 8 + 4х
аналогично
Пусть х₁>х₂, у₁ = -8+4х₁; у₂ = -8+4х₂; тогда 4х₁>4х₂, т.к. умножали на положительное одно и то же число 4; -8+4х₁>-8+4х₂, т.к. к обеим частям добалили одно и то же число -8, вывод у₁>у₂, доказано.
2. 1) свои наибольшее и наименьшее значения линейная функция достигает на концах отрезка. т.е. наименьшее равно у(-2)= 1.5-2*6=
-10.5; наибольшее у(1)=1.5+6=7.5
2) квадратичная функция у(7)=11-49=-38-наименьшее значение на указанном отрезке.