, затемподгору. рыболов на подъеме шел со скоростью на 2 км/ч меньшей,чем на спуске. расстояние доозера рыболов за 1 ч,а на обратный путь он затратил 6 мин больше,чем на путь
доозера. найдите скорость при подъеме и спуке если расстояние между станцией и озером 5 км
Другие вопросы по теме Алгебра
Популярные вопросы
- Революционная волна после Первой мировой войны Назовите важнейшие...
2 - Президент США В. Вильсон писал: «Если победит Германия, то что...
2 - Покажите, какие государства и народы в наибольшей степени пострадали...
2 - Граф Сеченьи, австро-венгерский посол в Берлине, говорил канцлеру...
2 - Самым активным неметаллом среди элементов Ge , As, Se, Br является...
1 - Степень окисления фосфора в ортофосфорной кислоте H3PO4 равна...
1 - Составьте развёрнутый план ответа по теме «Причины Первой мировой...
3 - Почему США вступили в войну именно в 1917 г.?...
3 - 3а счёт каких качеств страны Западной Европы и США обеспечили себе...
1 - Когда возникли Антанта и Тройственный союз?...
3
Наверное, всё-таки на обратную дорогу он потратил на 5 минут больше
1 ч. 5 мин.=13/12 ч.
Пусть х км/ч - скорость на подъёме, тогда скорость на спуске - (х+2) км/ч. Пусть у км - расстояние от станции до вершины горы, тогда расстояние от вершины горы до озера - (5-у) км. На дорогу от станции до озера рыболов затратил y/x+(5-y)/(x+2) или 1 час; на обратную дорогу - (5-у)/х + у/(х+2) или 1,1 часа. Составим и решим систему уравнений:
Произведём подстановку:
Домножим второе уравнение на 12/25:
По теореме Виета корнями уравнения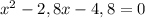 являются 4 и -1,2. Так как скорость не может быть отрицательным числом, получаем, что скорость на подъёме была равна 4 км/ч, а на спуске 4+2=6 км/ч.
являются 4 и -1,2. Так как скорость не может быть отрицательным числом, получаем, что скорость на подъёме была равна 4 км/ч, а на спуске 4+2=6 км/ч.
Путь от станции до вершины (4^2-3*4)/2=2 км, от вершины до озера 5-2=3 км.
ответ: скорость на подъёме 4 км/ч, скорость на спуске 6 км/ч.