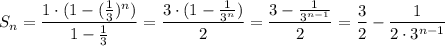Запишите выражение для нахождения суммы первых n членов прогрессии (bn) если : а)b1=1,q=5; б)b1=1,q=1/3 ' решить '
Другие вопросы по теме Алгебра
Популярные вопросы
- Каковы перспективы экономического развития польши?...
3 - Запишіть формулу азона та обчисліть його марекулярну масу...
2 - Між Києвом і Сумами є міста Прилуки і Ромни. Від Києва до Ромонів...
3 - с примером , алгебра 9 класс...
2 - Визначте слова іншомовного походження, запишіть їх групами за...
3 - РАСПАД ЗОЛОТОЙ ОРДЫ И ЕГО ПОСЛЕДСТВИЯ. Выполнить краткий конспект...
2 - Сказку Л.Чарской «Три слезинки королевны». У сказки печальный...
1 - 10 тапсырма. Берілген сөйлемдерден мәтін құра....
3 - Сочинение дорога Васи в дурном общество...
3 - 1. Те, кто показывает в сравнительной таблице особенности хозяйства...
2
Сумма первых n членов геометрической прогрессии: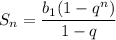
a)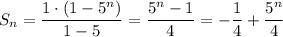
б)