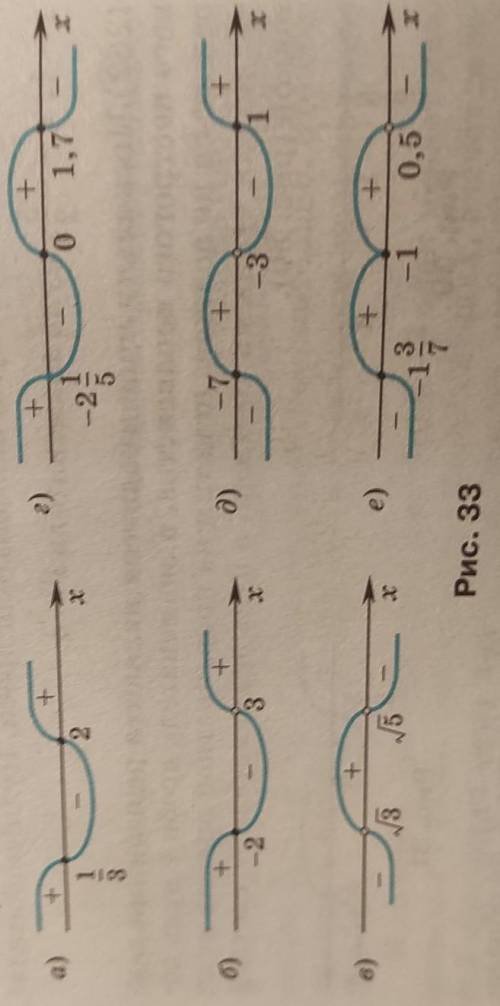
Запишите неравенство f(x) ≥ 0, при решении которого был сделан рисунок 33, и укажите промежутки, на которых значения f(x): а) положительны;
б) отрицательны;
в) неположительны;
г) неотрицательны.
Другие вопросы по теме Алгебра
Популярные вопросы
- Выберите один ответ: 1. на русском языке обязаны говорить все, кто собирается...
2 - Задание 1. Спишите предложения, заполните пропуски, вставленные слова...
2 - Укажите жанр произведения Пришвина Кладовая Солнца...
2 - Какие инструменты используются для создания 3D рисунка (несколько названий...
1 - 1. Дана соляная кислота, а также набор следующих реактивов: растворы...
3 - Длина волны фиолетового света составляет 380 нм. Постоянная Планка равна...
3 - Напиши эссе, выразив свое мнение по теме: ученики должны обязательно...
3 - A) Изобразите окружность, соответствующей уравнению (х + 4)^2 + (у –...
1 - Куда так,кумушка,бежишь ты без оглядки?»- Лисицу спрашивал Сурок.2 «...
3 - Сумма двух чисел равна 70. Найдите эти числа, если одно из них больше...
2
На рисунке видно, что график функции f(x) находится ниже оси Ox (то есть f(x) < 0) на промежутке от x = -5 до x = -3 и от x = 1 до x = 3.
Следовательно, неравенство f(x) ≥ 0 будет иметь вид:
(x ≤ -5) ∪ (-3 ≤ x ≤ 1) ∪ (3 ≤ x)
Теперь разберемся по пунктам:
а) Промежутки, на которых значения f(x) положительны, соответствуют промежуткам, на которых f(x) > 0. Исходя из рисунка 33, мы видим, что значения функции положительны на промежутках от x = -3 до x = 1 и от x = 3 до бесконечности: (-3 < x < 1) ∪ (3 < x < ∞).
б) Промежутки, на которых значения f(x) отрицательны, соответствуют промежуткам, на которых f(x) < 0. Исходя из рисунка 33, мы видим, что значения функции отрицательны на промежутках от x = -5 до x = -3 и от x = 1 до x = 3: (-5 < x < -3) ∪ (1 < x < 3).
в) Промежутки, на которых значения f(x) неположительны, соответствуют промежуткам, на которых f(x) ≤ 0. Исходя из рисунка 33, мы видим, что значения функции неположительны на промежутках от x = -5 до x = 1: (-5 < x ≤ 1).
г) Промежутки, на которых значения f(x) неотрицательны, соответствуют промежуткам, на которых f(x) ≥ 0. Мы уже определили ранее, что значения функции неотрицательны на промежутках от x = -3 до x = 1 и от x = 3 до бесконечности: (-3 ≤ x ≤ 1) ∪ (3 ≤ x).