Запишите координаты вершин параболы, укажите направление ее ветвей и постройте графики функций (13.4—13.5):
1) у = х²+ 4;
2) у = х² – 2;
3) у = -х² + 1,8;
4) у = -х²– 0,5;
5) у = х²– 1,4;
6) у = х²+ 1,5.
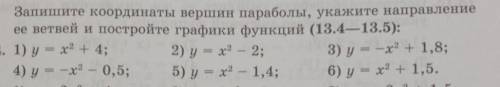
Другие вопросы по теме Алгебра
Популярные вопросы
- Какой пояс пересекает Южную Америку на севере и на юге?...
3 - Решите вариант надо, за все решённые задания...
1 - MN - диаметр окружности. Дуга NK на 1 2 0 ∘ больше дуги KM. Дуга NE...
1 - Какое известное средневековые извещения характеризует только от жизни...
3 - . Егер: 1) у = -x + 10 және у = 8,1; 2) у = 9,7 – 1,6x жәнеу = -6,3...
2 - Чему равно давление под малым поршнем? Под большим поршнем?...
3 - Не по интернету!) 1. Исток: 2. Устье: 3. Правые притоки: 4. Левые...
3 - Составте отзыв к рассказу белогрудка очень не из интернета...
1 - Частица обладает зарядом q=−1,168⋅10−16 Кл. Избыток или недостаток...
1 - Упражнения и задания: ТОЛько 3 во с текстом 1. Прочитайте текст. Определите...
1
Для решения данной задачи мы будем использовать стандартную формулу для параболы: у = ах² + bх + c.
Для начала, нам нужно определить коэффициенты a, b и c для каждой параболы по данным уравнениям.
1) В параболе у = х² + 4:
a = 1, b = 0, c = 4.
2) В параболе у = х² – 2:
a = 1, b = 0, c = -2.
3) В параболе у = -х² + 1,8:
a = -1, b = 0, c = 1,8.
4) В параболе у = -х² – 0,5:
a = -1, b = 0, c = -0,5.
5) В параболе у = х² – 1,4:
a = 1, b = 0, c = -1,4.
6) В параболе у = х² + 1,5:
a = 1, b = 0, c = 1,5.
Теперь, с помощью коэффициента a мы можем определить направление ветвей парабол.
Если а > 0, то ветви параболы открываются вверх.
Если а < 0, то ветви параболы открываются вниз.
Теперь рассмотрим каждую параболу и построим ее график.
1) Парабола у = х² + 4:
Решение:
a = 1 > 0, поэтому ветви параболы открываются вверх.
Для построения графика нам нужны координаты вершины параболы, которые можно найти так: х_вершины = -b / (2a), а у_вершины = у(x_вершины).
В данном случае b = 0 и a = 1, поэтому х_вершины = 0 / (2*1) = 0.
Подставим найденное значение х_вершины в уравнение: у_вершины = 0² + 4 = 4.
Таким образом, координаты вершины параболы - (0, 4).
Теперь построим график параболы, используя полученные значения:
- поместим точку вершины параболы (0, 4) на график,
- проведем параболу вверх через эту точку.
2) Парабола у = х² – 2:
Решение:
a = 1 > 0, поэтому ветви параболы открываются вверх.
Найдем координаты вершины параболы:
х_вершины = -b / (2a) = 0 / (2*1) = 0,
у_вершины = у(x_вершины) = 0² – 2 = -2.
Координаты вершины параболы - (0, -2).
Построим график параболы, используя полученные значения:
- поместим точку вершины параболы (0, -2) на график,
- проведем параболу вверх через эту точку.
3) Парабола у = -х² + 1,8:
Решение:
a = -1 < 0, поэтому ветви параболы открываются вниз.
Найдем координаты вершины параболы:
х_вершины = -b / (2a) = 0 / (2*(-1)) = 0,
у_вершины = у(x_вершины) = -(0)² + 1,8 = 1,8.
Координаты вершины параболы - (0, 1,8).
Построим график параболы, используя полученные значения:
- поместим точку вершины параболы (0, 1,8) на график,
- проведем параболу вниз через эту точку.
4) Парабола у = -х² – 0,5:
Решение:
a = -1 < 0, поэтому ветви параболы открываются вниз.
Найдем координаты вершины параболы:
х_вершины = -b / (2a) = 0 / (2*(-1)) = 0,
у_вершины = у(x_вершины) = -(0)² – 0,5 = -0,5.
Координаты вершины параболы - (0, -0,5).
Построим график параболы, используя полученные значения:
- поместим точку вершины параболы (0, -0,5) на график,
- проведем параболу вниз через эту точку.
5) Парабола у = х² – 1,4:
Решение:
a = 1 > 0, поэтому ветви параболы открываются вверх.
Найдем координаты вершины параболы:
х_вершины = -b / (2a) = 0 / (2*1) = 0,
у_вершины = у(x_вершины) = (0)² – 1,4 = -1,4.
Координаты вершины параболы - (0, -1,4).
Построим график параболы, используя полученные значения:
- поместим точку вершины параболы (0, -1,4) на график,
- проведем параболу вверх через эту точку.
6) Парабола у = х² + 1,5:
Решение:
a = 1 > 0, поэтому ветви параболы открываются вверх.
Найдем координаты вершины параболы:
х_вершины = -b / (2a) = 0 / (2*1) = 0,
у_вершины = у(x_вершины) = (0)² + 1,5 = 1,5.
Координаты вершины параболы - (0, 1,5).
Построим график параболы, используя полученные значения:
- поместим точку вершины параболы (0, 1,5) на график,
- проведем параболу вверх через эту точку.
На данном этапе мы рассмотрели все заданные параболы, определили их вершины, направление ветвей и построили их графики. Если у тебя остались какие-то вопросы, не стесняйся задавать!