Задано систему уравнений 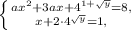 где x, y - переменные, а - произвольная постоянная. 1. Решите систему, если а = 0.
где x, y - переменные, а - произвольная постоянная. 1. Решите систему, если а = 0.
2. Определите все решения заданной системы в зависимости от значений а.
Другие вопросы по теме Алгебра
Популярные вопросы
- Наступила осень с (не)скончаемыми дождями, мокрыми дорогами, с тоской по вечерам....
2 - Сколько миллиметров в диаметре монеты достоинством 20 тетри?...
2 - Якими шляхами забезпечується гормональна регуляція функції організму: а)передачі...
3 - Вкоробці знаходяться 15 білих і 24 зелених кульок. яка ймовірність того що навмання...
1 - В1 баке бензина вдвое больше чем во втором если перелить из 1 бака во 2 бак...
1 - Все ! в противоположных, наиболее удаленных друг от друга вершинах куба находятся...
3 - Через яку з точок проходить графік рівняння: 4x+5y=20? а) а(0; -4); б) в(1;...
3 - Главная мысль произведения телефон. корней чуковский....
2 - 28х(в кубе)+3х(в квадрате)+3х+1=0 разложить на множители...
3 - Хранившееся на складе зерно имело влажность 28%. после просушивания влажность...
2
Задано систему уравнений
{ ax² +3ax +4^(1+√y) =8 ; x+2*4^y = 1 где
x, y - переменные, а - произвольная постоянная . ( параметр ) .
1. Решите систему, если а = 0.
2. Определите все решения заданной системы в зависимости от значений а.
ответ 1 : если а = 0 , → ( - 3 , 0,25) . ,
ответ 2 :
одно решение: если а = -2/3 → ( - 3 , 0,25) ,
два решения: если а ≠ 0 и а ≠ -2/3
(x₁ ; y₁ ) → ( - 3 , 0,25) и (x₂ ; y₂ ) ⇒ (2/a ; 0,25( log₂ ( (a -2)/ 2a ) )²
Объяснение: ОДЗ : y ≥ 0
{ ax² +3ax +4^(1+√y) =8 ; x+2*4^y = 1. ⇔
{ ax² +3ax +4^(1+√y) =8 ; 2x+4^(1+√y) = 2.
{ ax² +3ax + 4^(1+√y) =8 ; 4^(1+√y) = 2 -2x . ⇒
ax² +3ax +2 -2x = 8
ax² -(2 -3a)x - 6 = 0
1. Если а = 0 (линейное уравнение)
0 -2x - 6=0 ⇒ x = - 3 ;
4^(y) = (1 -x)/2 ⇒ 2^(2√y) = 2¹ ⇔2√y) = 1 ⇔
√y = 0,5 ⇒ y = 0,25 ответ 1 : (-3 ; 0,25)
2. Если а ≠ 0 имеем квадратное уравнение
ax² - (2-3a)x -6 = 0 дискриминант которого
D = ( 2 -3a )² - 4*1(-6) = ( 2 +3a )² ≥ 0 , следовательно данное кв. уравнение для любого значения параметра a имеет решение.
2.а одно решение , если D = 0 , т.е. при а = -2/3
x₀ = (2-3a)/2a = 1/a - 3/2 = - 3/2 -3/2 = - 3 ⇒ y₀ = 0,25
два решения, если D ≠ 0 , т.е. при { а ≠ -2/3 ; а ≠ 0 }
x₁ =( 2 -3a) - (2 +3a ) ) / 2a = -3 ⇒ y₁ = 0,25 ;
- - - - - - - - - - - -
x₂ = ( 2 -3a) + (2 +3a ) ) / 2 a = 2/a ;
4^(√y₂) = (1 -x₂) /2 ⇔ 2^(2√y₂) = (a -2)/2a
* * * (a- 2)/2a >0 ⇒ a ∈ (- ∞ ;0) ∪ (2; ∞) * * *
2√y₂ = log₂ ( (a -2)/2a ) ⇔ √y₂ =0,5( log₂ ( (a -2)/2a )
имеет решения , если log₂ ( (a -2)/ 2a ) ≥ 0
(a -2)/ 2a ) ≥ 1
(a - 2) / 2a) - 1 ≥ 0
(a - 2 - 2a) /2a ≥ 0
(a + 2)/ a ≤ 0
+ + + + + + [ -2] - - - - - (0) + + + + + + +
a ∈ [ -2 ; 0 ) , учитывая а ≠ -2/3
получается a ∈ [ -2 ; -2/3 ) ∪ (-2/3 ; 0 )
y₂=0,25( log₂ ( (a -2)/ 2a ) )²
* * * 3 раза повторяется решения ( - 3 , 0,25) * * *