Задание на картинке ⬆️⬆️⬆️
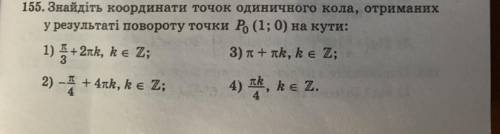
Другие вопросы по теме Алгебра
Популярные вопросы
- 2.Определи к какому жанру детского фольклора относится произведение:Катилось яблочко...
2 - Обьясните постановку запятых на цифрах 16,17 Здесь господствовала та обстановка...
3 - определи количество цифр в частном не выполняя вычислений 34020/2 ; 304020/20;...
1 - АЛГЕБРА 8 КЛАСС БИЛИМ ЛЭНД Я УЖЕ НЕ ЗНАЮ ЧТО ДЕЛАТЬ...
3 - Какое логическое выражение равносильно выражению ¬(A ∨ ¬B ∨ C) ¬A ∨ B ∨ ¬C A ∧...
3 - нужно тут условие и формулу написать а ответ не нужен....
2 - 1 Из скольких и каких строф состоит стихотворение? 2 Выпиши эпитеты.3 Выпиши олицетворения.4...
1 - Определи координаты точек А, B, C, D...
1 - В ∆ABC: ∠C = 90°, ∠B = 60°, AC = 5. Вычисли BC....
3 - Во сколько раз увеличилось количество мануфактур во времена правления Екатерины...
2
Объяснение:
P₀( 1 ; 0 ) ; 1 ) α = π/3 + 2πk , kЄ Z ;
P₁ ( cosπ/3 ; sinπ/3 ) = P₁ ( 1/2 ; √3/2 ) ; додаючи повні оберти ( додатні
або від"ємні ) , точка P₁ матиме ті самі координати ;
P₀( 1 ; 0 ) ; 2 ) α = - π/4 + 4πk , kЄ Z ;
P₂( cos( - π/4) ; sin(- π/4) ) = P₂( √2/2 ; - √2/2 ) ; 4π - це два повні оберти ,
тому , додаючи повні оберти ( додатні або від"ємні ) , точка P₂ матиме ті самі координати .