Задание на фото найти х/y можно, если будут найдены х и y
а можно ли найти х/y, не находя значения х и y?
Другие вопросы по теме Алгебра
Популярные вопросы
- Яблоко это имя а) прилаг одущ б) сущес неодуш в) сущес одуш г) плаг неодуш...
3 - Fill in the correct form of the present perfect tense. 1. The solar system...
3 - Как переводится слово школа?...
3 - В сколько раз 15^5 больше чем 5^6 * 27 ?...
1 - Література зарубіжна на літо 7 клас Відповіді...
3 - Make sentences with *forget* with 5 tense positive negative and interrogative...
3 - За рисунком знайдіть кут х (О - центр кола), a=21°, b=49°....
2 - Проблемы рассказа Железников . Жизнь и приключение чудака....
1 - 3. Охарактеризуйте отношения России с великими державами Европы: Англией, Францией,...
3 - РЕШИТЬ С ОБЬЯСНЕНИЕМДАЮ ЛУЧШИЙ ОТВЕТ знайдіть суму двоцифрових чисел які під...
1
х/у=(-3+-sqrt(5))/2
Объяснение:
Так как D<0 , то действительных корней нет . Система не имеет решений .
ответ: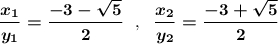 .
.