Задание 2. Докажите, что разность квадратов двух последовательных нечетных чисел
делится на 8.
Для начала составим выражение, о котором говорится в задании. Если четное число
можно записать при переменной как 2, то нечетное число будет выглядеть как
2n + 1.
1-ое нечетное число: 2n + 1
2-ое нечетное число: 2n + 3
Разность квадратов этих чисел: (2 + 3)
2 − (2 + 1)
2
Теперь необходимо доказать, что данное выражение кратно 8. Попробуйте сделать это
самостоятельно. Здесь неважно то, как вы начнете действовать: вы можете
воспользоваться формулой разности квадратов, а можно взять и у данное
выражение.
Задание 3. Докажите, что если к произведению трёх последовательных целых чисел
прибавить среднее из них, то полученная сумма будет равна кубу среднего числа.
Подсказка:
Рассмотрим каждое выражение, о котором говорится в задаче.
Первое число:
Второе число: ( n+ 1)
Третье число: (n + 2)
Их произведение:n ( n+ 1)(n + 2)
Прибавим среднее число и получим: (n + 1)(n + 2) + (n + 1)
Куб среднего числа: (n + 1)
3
Теперь можем составить тождество, которое необходимо доказать:
n(n + 1)( n+ 2) + (n + 1) = (n + 1)3
Другие вопросы по теме Алгебра
Популярные вопросы
- Кусок льда массой 0,6 кг нагревают от −29°C до −5°C, затрачивая при этом...
3 - всё ни как не могу сделать...
3 - Төмендегі сөйлемдерді көшіріңдер, етістіктерді тауып, дара, күрделі түрін...
1 - Плачу 30р. рублей за выполнение этого теста (сразу оставьте ваш QIWI)...
1 - 1. Как называется опера Н. А. Римского-Корсакова о новгородском гусляре,...
2 - Мәтіннен етістіктерді табыңдар, оларға сұрақ қойыңдар. А тарихын зерттеп...
1 - умоляю.Кстати с новым годом желаю всем вам и вашим родным счастья и всего...
3 - Периметр параллелограмма равен 44 см. Найдите стороны параллелограмма,...
3 - 2.Задание для обратной связи. Распредели данные слова в три столбика.Юрист,...
2 - 5-тапсырма. Мәтіннің мазмұнына сүйене отырып, кейіпкерлерге жекежеке мінездеме...
1
Если число можно представить в виде произведения , где одним из множителей является 8, то это число делится на 8 .
Если к произведению трёх последовательных чисел прибавить среднее из них, то полученная сумма равна кубу среднего числа.
Задание 2
Обозначим первое число как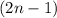 , а следующее за ним как
, а следующее за ним как 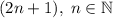 . Раскроем разность квадратов по формуле
. Раскроем разность квадратов по формуле 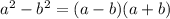 :
:
Один из множителей делится на 8, а значит, и всё число делится на 8.
Задание 3
Запишем три последовательных числа как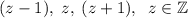 . Составим выражение из условия:
. Составим выражение из условия:
Что и требовалось доказать.