Задача 5. Найдётся ли среди чисел 1, 11, 111, ..., в десятичной записи которых
используется только цифра «1» число кратное 2021?​

Да, найдется

Объяснение:

Рассмотрим остатки отделения чисел вида (10^n-1)/9 на 2021. Количество возможных остатков конечно, а это значит, что найдутся такие числа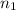   и 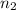 , для которых остатки от деления равны. Поэтому если вычесть одно число из другого, то остаток от деления полученной разницы на 2021 будет равен 0. Полученное число будет иметь вид 11...11*10^n. Но  2021 не делится ни на 5, ни на 2. Из этого следует, что число 11..11 делится на 2021.

Теорема Эйлера позволяет найти длину числа 11..11, которое делится на 2021. Это 1932.  Но это не минимальное n, (10^966-1)/9 тоже делится на 2021.