Задачі з параметрами, 11 клас

Другие вопросы по теме Алгебра
Популярные вопросы
- Благаю розв яжіть 972впр ...
1 - 1) Чому дорівнює добуток коренів рівняння х²-7х+3=0?(виберіть букву та поясніть...
3 - биссектриса внешнего угла при вершине B треугольника ABC параллельна стороне...
2 - В чём причина зависимости сопротивления всех видов проводника от температуры...
3 - Поясни, чому класифікацію можна вважати результатом систематики очень ...
1 - каково взаимное расположение касательных к окружности, проведенных через...
3 - Өлең маһмұнын оқы ,аста сызылған сөздерді тура және ауыспалы мағынасын...
3 - Математика теңдеулерді шеш у÷4=535÷5...
3 - 1-тапсырма 90 бет. Сұрақтарға жауап бер. 1. Қазақтың қандай жазушыларын...
2 - Запишіть подані словосполучення у давальному відмінку однини.....
2
Объяснение:
Пусть уравнение имеет некоторый корень r. Тогда его второй корень должен быть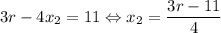 . По теореме Виета:
. По теореме Виета:
Решим второе уравнение: