1. Алгебра
  2. За победу в шахматной

За победу в шахматной партии начисляют 1 очко, за ничью ─ 0,5 очка, за проигрыш ─ 0 очков. В турнире принимают участие m мальчиков и d девочек, причём каждый играет с каждым дважды. Сколько девочек могло принимать участие в турнире, если известно, что их в 7 раз меньше, чем мальчиков, и что мальчики набрали в сумме ровно в три раза больше очков, чем девочки
Запишите решение и ответ.

chapa00 chapa00    2   22.02.2020 19:52    55

Ответы
карина0212 карина0212  11.10.2020 11:22

Для Нечётных:

\left.\begin{matrix}\begin{matrix}M-14k+7\\ D-2k+1\end{matrix}\end{matrix}\right|\left.\begin{matrix}\begin{matrix}3x\\ x\end{matrix}\end{matrix}\right|\begin{matrix}7d\\ d\end{matrix}

Всего: 16k+8=8d

Всего партий: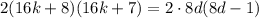2(16k+8)(16k+7)=2\cdot 8d(8d-1)

256k^2+112k+128k+56=64d^2-8d\\32k^2+30k+7=8d^2-d\\(2k+1)(16k+7)=d(8d-1)

d=2k+1 или d=16k+7 или 8d-1=2k+1=>d=2k+1

d=\frac{k+1}{4} - не подходит

Для Чётных:

\left.\begin{matrix}\begin{matrix}M-14k\\ D-2k\end{matrix}\end{matrix}\right|\left.\begin{matrix}\begin{matrix}3x\\ x\end{matrix}\end{matrix}\right|\begin{matrix}7d\\ d\end{matrix}

Всего: 18k

Всего партий: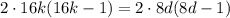 2\cdot 16k(16k-1)=2\cdot 8d(8d-1)

256k^2-16k=64d^2-8d\\2k(16k-1)=d(8d-1)

\left.\begin{matrix}d=2k\Rightarrow 16k-1=16k+1 (+)\\d=16k-1\Rightarrow 2k=128k-7 (-)\\8d-1=2k\Rightarrow d=64d-9 (-)\\8d-1=16k-1\Rightarrow 2k=2k (+)\end{matrix}\right|\Rightarrow d=2k

ответ: Девочек могло быть сколько угодно

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
YeezyM YeezyM  29.06.2019 18:00
Сумма двадцати пяти членов арифметической прогрессии равна 525 найдите разность прогрессии если известно что её первый член равен -51...
yuyornevzkoxkdhd543 yuyornevzkoxkdhd543  29.06.2019 18:00
Выполните указанные действия (√7-2)(√7+2)...
so4tfx so4tfx  29.06.2019 18:00
Построить график функции y=x^2+4x+4. при каких значениях x значениях y положительные?...
MariMQ MariMQ  29.06.2019 18:00
Найдите наибольшее значение выражения x^2+3y^2 если x^2+y^2=1...
МилаяПолина МилаяПолина  29.06.2019 18:00
Найдите площать фигуры, ограниченной отрезками прямой y = 1 - 2x и графиком функции y= x^2 - 5x - 3...
zFast88 zFast88  29.06.2019 18:00
Вычеслите 2 в третей степени - 2 в четвёртой степени...
surgut186rus surgut186rus  04.12.2020 15:38
Берілген функциялардын графиктерін сəйкестендіріңіздер:​...
garanina2005 garanina2005  04.12.2020 15:38
Вычислите значение выражения ​...
sevasik12 sevasik12  04.12.2020 15:38
Запишите формулу линейной функции, график которой параллелен графику функции y=x-5 и проходит через точку A(2;3)....
igorlenkov2017 igorlenkov2017  04.12.2020 15:38
Промежутки возрастания и убывания функции y=2x^3-3x^2-36x+40​...

Популярные вопросы