за ответ решите a)1+cos α - sin α
б)1-sin α - cos α
α—это альфа
Другие вопросы по теме Алгебра
Популярные вопросы
- Сделать звуко буквенный разбор слова подъем...
3 - Какая связь между термином растение и одним из четырёх терминов, ниже. опредилите...
1 - Правильные формы числительных использованы в словосочетаниях в восьмистах экземплярах...
2 - На рынок 640кг яблок: 35 ящиков по 8 кг, а в остальных ящиках по 6 кг. сколько всего...
1 - Школьники вместе с родителями расчистили от мусора пустырь за школой и засадили...
3 - Как построить высоты прямого тупого и острого угла?...
1 - Товар цена которого до распродажи была 5000 рублей, уценили на 5%. чему равна новая...
3 - Морфологический разбор слова: гроям...
3 - Найдите силу тяжести, действующую на брусок объемом 500 см3. плотность бруска 4000...
2 - В1712 году санкт - петербург стал столицей россии. подчеркни какой город был столицей...
3
Формулы.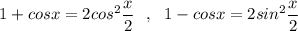 ,
,