1. Алгебра
  2. Язнаю, что для вас это сущий

Язнаю, что для вас это сущий пустяк)) 1) найдите значение производной функции f(x)=x^3 - 4 в точке в точке хо=2 2) запишите уравнение касательной к графику функции f(x)=cos^2 x в точке с абсциссой хо=п\2

Евдокия47 Евдокия47    1   20.05.2019 22:40    0

Ответы
ДЕСПАСИТО18 ДЕСПАСИТО18  01.10.2020 01:24

1) f'(x)=3x^2;

f'(x0)=3*4=12

 

2) f(pi/2)=y0=0;

f(x)=(1+cos2x)/2

f'(x)=-sin2x

k=f'(pi/2)=0

 

ур-е кас y=y0+k(x-x0)

y=0

ПОКАЗАТЬ ОТВЕТЫ
countrestrikegl countrestrikegl  01.10.2020 01:24

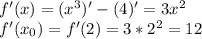
1)f'(x)=(x^3)'-(4)'=3x^2\\f'(x_{0})=f'(2)=3*2^2=12

2)Уравнение касательной: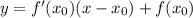y=f'(x_{0})(x-x_{0})+f(x_{0})

Производная:

f'(x)=(cos^2x)'=(cosx*cosx)'=\\=(cosx)'*cosx+cosx*(cosx)'=\\=(-sinx)*cosx+cosx*(-sinx)=-sinx*2cosx=-2sin2x. 

Или можно проще:

f'(x)=(cos^2x)'*(cosx)'=2cosx*-sinx=-2sin2x

f'(x_{0})=f'(\frac{\pi}{2})=-2sin({\frac{2*\pi}{2})=-2sin180=0

f(x_{0})=f(\frac{\pi}{2})=cos^2(\frac{\pi}{2})=cos^290=0

Подставим значения в уравнение касательной:

y=0*(x-\frac{\pi}{2})+0=0

 

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ilia62002 ilia62002  23.05.2019 18:10
Выделите квадрат двучлена из квадратного трехчлена х2-6х-2...
profi14 profi14  23.05.2019 18:10
Морская вода содержит 5 % соли а) сколько соли в стакане морской воды (200г) ? б) какое количество морской воды надо взять, чтобы в ней содержалось 200 г соли?...
OnAcHaYa2o2 OnAcHaYa2o2  23.05.2019 18:10
Представьте произведение в виде степени: 2^5*64...
Alla03u03 Alla03u03  23.05.2019 18:10
Сколько килограммов сливочного масла можно полуяить из 1000 кг молока жирностью 4,5%, если содержание жира в масле составляет в среднем 75%?...
бог100001 бог100001  10.04.2020 09:12
Преобразуйте произведение в сумму: соs40•cos20...
long6 long6  10.04.2020 09:12
Решите уровнение 3(2x-4)=2x(5x+9)​...
sasha235sasha sasha235sasha  10.04.2020 09:13
Самостоятельная работа 1. Найдите сумму первых 12 членов арифметической прогрессии (а), если а = 3, d = 2. 2. Найдите сумму первых 20 членов арифметической прогрессии -3, -2,-1,...
Юлия0981 Юлия0981  10.04.2020 09:13
Решите задачу составив уравнение найдите сумму четырех последовательных натуральных чисел, если известно, что произведение наибольшего и наименьшего из них на 2 произведение средних...
Элина1111111111112 Элина1111111111112  10.04.2020 09:13
Не выполняя построения, найдете координаты точек пересечения с осями координат графика кравнения 1).х^2+у=36. 2) х^2+у^2=25...
думайй думайй  10.04.2020 09:13
Автомобиль долженпроехать 600 км. Двигаясьсо скоростью у км ч, онзатратит на этот путь tч.Задайте формулойзависимость временидвижения от скорости.​...

Популярные вопросы