Является ли счетным множество a∪b, если
a={x, x= $\sqrt{n^5}$ , n - натуральные числа}
b={x, x - корень уравнения $a_{n}x^n+a_{a-n}x^{n-1}++a_{1}x+a_{0}=0$ принадлежащий целым числам}

Ответы

kolody71p0aje8 07.10.2020 09:50

Теорема. Конечное объединение счетных множеств дает счетное множество.

По сути нужно доказать, что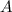 и и 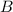являются счетными. Докажем счетность множества .

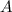Очевидно, что между каждым элементом множества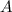 можно поставить взаимоднозначное соответствие с множеством натуральных чисел, которое как известно является счетными, т.е. множество 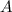- счетно.

Докажем теперь счетность множества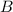

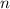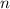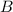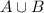Согласно основной теореме алгебры, полином -ой степени имеет различных корней, т.е., очевидно, что количество полиномов является счетным, поскольку для каждого полинома можно установить биекцию множеству натуральных чисел, причем каждый полином имеет конечное число корней, тогда по выше сказанной теореме множество - счетно.