1. Алгебра
  2. Яким має бути m, щоб

Яким має бути m, щоб корені рівняння
4x ^{2} - (3m + 1)x + m - 2 = 0
були розміщенні між числами
-2 та 4?
іть, дуже потрібно, 50 і! ​

nik180208 nik180208    2   21.12.2019 23:06    2

Ответы
Нафунька Нафунька  23.08.2020 11:48

m\in (-\dfrac{16}{7}; \dfrac{58}{11})

Объяснение:

4x ^{2} - (3m + 1)x + m - 2 = 0

Найдем корни:

D = {(3m + 1)}^{2} - 4 \times (m - 2) \times 4 = 9 {m}^{2} - 10m + 33 \\ \sqrt{D} = \sqrt{9 {m}^{2} - 10m + 33} \\ x12 = \frac{3m + 1 + - \sqrt{9 {m}^{2} - 10m + 33} }{8}

А теперь получили 2 неравенства. Если я правильно понимаю, что тут написано, а я не использую переводчик, знак неравенства строгой. Если не понимаю, то нестрогий:

- 2 < \frac{3m + 1 + - \sqrt{9 {m}^{2} - 10m + 33} }{8} < 4

Откуда находим m:

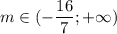
1) m\in (-\dfrac{16}{7}; +\infty)

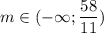
2) m\in (-\infty ; \dfrac{58}{11})

А теперь ищем пересечение!

m\in (-\dfrac{16}{7}; \dfrac{58}{11})

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Xtanev Xtanev  24.07.2019 18:50
При каком значении к график функции y=kx-6 проходит через точку а (-2; 20)...
Windsorcastle Windsorcastle  24.07.2019 18:40
Решите уравнения: а)у^2-100=0 б)z^2-625=0 в)t^2-1=0...
vika200920001 vika200920001  24.07.2019 18:40
Разложите на множители.ответ по действиям.(x+1)+x(x+1)....
sevara221 sevara221  24.07.2019 18:40
При каком значении k, график функции y=kx-4, проходит через точку b(14; -32). развернутый ответ!...
Cosb Cosb  24.07.2019 18:40
(с+6)^2-с(с+12) выражение; уровнение (х-7)^2-(х-4)(х+4)=65...
tatsux2010 tatsux2010  28.02.2021 17:25
Разложите на множители (х-5)в квадрате +(х-5)(х...
Топовая20171 Топовая20171  28.02.2021 17:22
A^2-2ab+b^2-ac+bc; a^2-2ab+b^2-3a+3b; m^2+6mn+9n^2-m-3n; (b-c) (b+c)-b(b+c); a^2-9b^2+a-3b; 4a^3-ab^2;...
annalonina annalonina  28.02.2021 17:22
Упростите выражения: а) cos(α - β) - cos(α + β) ( ); б) 020.jpg ( )....
Якрутой111 Якрутой111  28.02.2021 17:22
Аб+ас=а(б+с) разложите на множители​...
Zaya191 Zaya191  18.05.2019 20:30
Два автомобиля выезжают одновременно из одного города в другой. скорость первого на 20км/ч больше скорости второго и поэтому первый автомобиль приезжает на место...

Популярные вопросы