1. Алгебра
  2. Як з чисел 2^121, 7^44,

Як з чисел 2^121, 7^44, 64^22, 17^33 найбільше?

Rita53 Rita53    1   08.01.2022 18:47    0

Ответы
lizazimovets1 lizazimovets1  08.01.2022 18:50

Воспользуемся свойством степени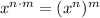 x^{n\cdot m}=(x^{n})^{m}  .

2^{121}=2^{11\cdot 11}=(2^{11})^{11}=2048^{11}7^{44}=7^{4\cdot 11}=(7^4)^{11}=2401^{11}64^{22}=64^{2\cdot 11}=(64^2)^{11}=4096^{11}17^{33}=17^{3\cdot 11}=(17^3)^{11}=4913^{11}

Функция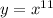  y=x^{11}   возрастающая при  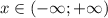x\in (-\infty ;+\infty ) , поэтому при чем больше основание степени, тем больше значение этой степени .

2048

Наибольшее число - это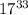   17^{33}  .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
новичок579 новичок579  02.12.2020 11:55
Постройте график функции у=2х-1. Найдите по графику: а) значение у при х=2 б) значение х при у=-1...
данил2908 данил2908  02.12.2020 11:55
На рисунке изображен график линейной функции. Какие координаты имеют точки пересечения этого графика с осями координат? За раннее...
GolubinoeMoloko GolubinoeMoloko  02.12.2020 11:55
Решение системы линейных уравнений с двумя переменными графическим Урок 1 Реши систему уравнений графическим (2(х-у)-х=4-3у,)х=2(у-10)-хответ: x = y =...
Fluttershy0 Fluttershy0  02.12.2020 11:54
решить уравнения и неравенства...
versuspro99 versuspro99  02.12.2020 11:54
Функций задана формулой y = 1/3 x - 7 найдите а) значение функций значению аргументу равному 9 б) значение аргумента при котором значение функций равно - 8...
iragav30 iragav30  29.11.2021 13:49
. Составить каноническое уравнение: - эллипса, Если А, В - точки, лежащие на прямой. A(0,√3), B(√(14/3),1); - гиперболы, если k - угловой коэффициент, e - эксцентриситет....
Sasha7749 Sasha7749  29.11.2021 13:46
Найдите матрицу С= + 3 В ответ введите сумму элементов 2-го столбца матрицы С....
nikita140982ee nikita140982ee  29.11.2021 13:45
Побудуйте графік функції у = -х² + 6x - 5 та знайдіть: 1) область значень функції; 2) проміжок зростання та проміжок спадання функції ....
марго170 марго170  29.11.2021 13:44
велосипедист проехал 10 км за 0, 5 ч, затем ещё 40км за 1,5ч. определите среднюю скорость движения на всём пути...
zaec999 zaec999  29.11.2021 13:44
Доведіть,що 5³¹-25¹⁵ діляться на 20...

Популярные вопросы