я ничего не понимаю контрольная по алгебре 8 класс номер номер 6 и 7
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие средства хранения информации были первыми?...
1 - Раньше были бумажные деньги по 3 рубля и по 5( трешки и пятерки)...
1 - Как составить звуковую схему к словам для первого класса...
3 - Вкаком ряду из слов на месте пропуска иная,чем в других словах...
1 - Синтаксический разбор предложения: детское воображение превращало...
3 - Технология. какое технологическое свойство шелковых тканей необходимо...
3 - You shouldn t trick or вставить слово...
3 - Тело с высоты 4м бросают в горизонтальном направлении так, что...
2 - Вкаких городах и местностях происходят извержения вулканов?...
1 - Креволюций в странах европы не относится дата: а)1814-1815гг. в)1830-1831гг....
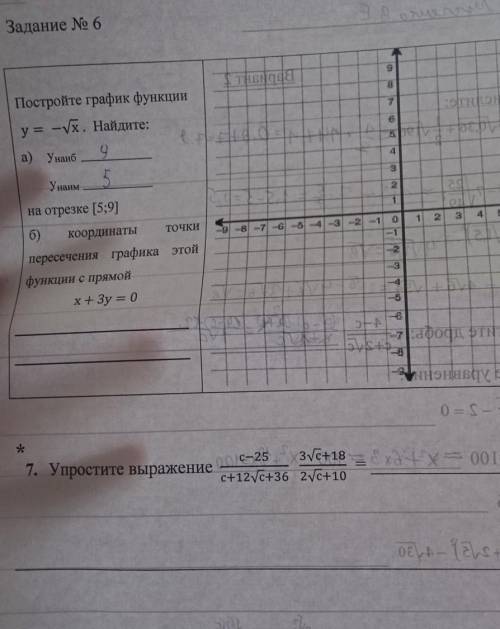
1
Объяснение:
а) На отрезке [5;9)
у(наиб) = -√5
у(наим) = - √9 = - 3
б) {y = -√x → { у = -√x
{x+3y = 0 → { y = -x/3
-√x = -х/3 → х = х²/9 → 9х = х² → х( х - 9) = 0
х₁ = 0, у₁ = 0
х₂ = 9, у₂ = -3
Две точки пересечения: О(0;0) и А(9;-3)
7. (√с -5)(√с + 5)/(√с + 6)² * 3(√с + 6)/2(√с +5) =
=3 (√с-5)/2(√с + 6)