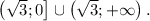Алгебра: Y=корень x/x^2-3 найдите область определения функции

Y=корень x/x^2-3 найдите область определения функции

Ответы

rot3 04.10.2020 04:15

$\displaystyle y=\sqrt{\frac x{x^2-3}}$

Знаменатель не должен равняться нолю, а подкоренное выражение должно быть не отрицательным. Условия для знаменателя будет учитываться при рассмотрении условия для выражения под корнем.

$\displaystyle \frac x{x^2-3} \ge 0$

Разложим выражение в знаменателе на множители с формулы сокращённого умножения: a²-b² = (a-b)(a+b).

$\diplaystyle 3=(\sqrt3)^2\\ \\ x^2-(\sqrt3)^2=(x-\sqrt3)(x+\sqrt3)$

Тогда имеем:

$\displaystyle \frac x{(x-\sqrt3)(x+\sqrt3)} \ge 0$

Решим неравенство с метода интервалов:

Отмечаем на координатной прямой точки, в которых выражения из числителя и знаменателя обращаются в ноль. И выкалываем те, что относятся к знаменателю (на ноль делить нельзя). Мы получили 4 интервала. Перед дробью знак положителен, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (нету чётных степеней, где знак может не измениться). Нас интересует, когда больше или равно нуля, поэтому выбираем интервалы с плюсом и учитываем их границы.

Получили:

$\displaystyle \sqrt3 \sqrt3$