Y=f(x)- периодическая функция с периодом t=4. известно что f(x)=3-x², если -2

а)

При -2<x≤2, графиком функции f(x) будет y=3-x². Это парабола, ветви направлены вниз, координата вершины (0;3). Найдём точки пересечения с осями координат:

x=0 ⇒ y=3-0²=3; (0;3)

y=0 ⇒ 3-x²=0; x²=3; x=±√3; (-√3;0), (√3;0).

Всё, что мы нашли находится в указанном промежутке. 3-(-2)²=3-2² - ординаты границ промежутка совпадают, период равен 4 ⇒ 2-4 = -2, поэтому график функции f(x) будет непрерывным. Таблицу точек для y=3-x² и график функции смотри в приложении.

б)

Нули для y=3-x² мы знаем, для f(x) будут такие же нули, но есть ещё период, поэтому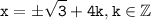 - ответ.

в)

Определим по графику.