Y"=3sqrt(y+1) решить, условие - найти частное решение диффиренциального уравнения, допускающего понижение порядка

Ответы

ousod 08.10.2020 20:19

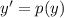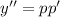Здесь правая часть уравнения зависит только от переменной у. Вводим замену y'=p(y) тогда y''=pp' , получаем

$pp'=3\sqrt{y+1}$ - уравнение с разделяющимися переменными

$\displaystyle \int pdp=3\int\sqrt{y+1}dy\\ \\ \dfrac{p^2}{2}=3\cdot \dfrac{2}{3}(y+1)^{3/2}+C_1~~~~\Rightarrow~~~ p=\pm\sqrt{4(y+1)^{3/2}+C_1}$

Выполним обратную замену

$y'=\pm\sqrt{4(y+1)^{3/2}+C_1}\\ \\ \displaystyle \int \dfrac{dy}{\sqrt{4(y+1)^{3/2}+C_1}}=\pm\int dx\\ \\ \\ \int \dfrac{dy}{\sqrt{4(y+1)^{3/2}+C_1}}=\pm\dfrac{x^2}{2}+C_2$

Последний интеграл не так уж и просто вычислить...

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

karyakinayulya 08.06.2020 12:25

Найдите наибольшее и наименьшее значения функции f (x) = 1+8x -x2 на промежутке [2; 5]....

madina20042004 08.06.2020 12:34

Дана равнобедренная трапеция ABCD. AB – большое основание трапеции и на ней взята точка E так, что угол ∠DEC стал равным углу при основании трапеции. Если DE=6, EC=10,...

Katekate2001lol 09.06.2020 00:36

НУЖНО ОТВЕТИТЬ В ТЕЧЕНИИ 5 ЧАСОВ. Побудуйте графік функції y= x2 + 6x +8 Користуючись графіком знайдіть 1) найменше значень функції2) проміжок, на якому функція набуває...

Sashakosix 08.06.2020 13:07

Приведите уравнение 4р + 7,9 = 5р – 2 к линейному: a)р = 5,9. b)p=0c)-p=-9.9d)9р = – 9,9; e)–р = 9,9;...

mokantatiana 08.06.2020 13:07

Найти значение выражения Фото...

raya323 08.06.2020 13:32

студентов при очной форме обучения могут заболеть короновирусом. На первом курсе учатся 120 человек. Сколько человек могут заболеть? Заранее...

Дайяник 17.08.2019 21:30

Постройте график функции y=-3\x+1 +2...

patoga79p00pc3 17.08.2019 21:30

25x-100=0 100x+25=0 -200x+100=0 200x-100=0 решить...

Wolffy 17.08.2019 21:30

Постройте график функции у+3х²-6х+2...

dimadi1 17.08.2019 21:30

Найти значения выражения : 10х2степени а0 степени при х=1/3×а=7...

Y"=3sqrt(y+1) решить, условие - найти частное решение диффиренциального уравнения, допускающего понижение порядка

Популярные вопросы