Y= 2 +15x +2х*корень из х найти точку max

Нет точки максимума

Объяснение:

Рассмотрим функцию

Так как в составе функции участвует квадратный корень, то область определений функции: x≥0, то есть D(y)=[0; +∞).

Чтобы найти экстремумы (локальные минимумы и максимумы) будем исследовать функцию с производной функции. Вычислим производную функции:

Так как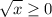 , то

для любого x∈D(y). Это означает, что данная функция монотонно возрастает в D(y). Отсюда следует, что у функции нет точки максимума.

Так как функция монотонно возрастает в D(y), то минимальное значение в D(y)=[0; +∞) принимает при x=0: y(0)=2.