Y= 1/3*x^3-x+3 исследовать функцию и построить график и если можно то
Другие вопросы по теме Алгебра
Популярные вопросы
- Выполните вычисление выражений удобным...
3 - 28 яким утворено слово пересісти ? а: суфіксальним б: безафіксним в: префіксальним...
2 - На столе лежат 60 палочек, имеющие длины 1, 2, 60. какое наименьшее количество...
2 - Двигатель внутреннего сгорания работает на нефти и много порции дровах бензине...
1 - При копра забивают сваю массой 70 кг. боек копра имеет массу 400 кг. при ударе...
2 - Визначте випаровуваність для м.херсона, якщо опадів там випадає 435 мм за рік,...
1 - Загадка про хуху моховинку (не ту что уже есть)...
1 - Срешением . нужно найти центр тяжести этого тела, 5 вариант...
2 - Втреугольнике авс отрезок аd=6 см и равен половине ав. найдите длину вс(в см),если...
1 - Pick out the names of persons in the following : (1) the boy saw his brother....
3
1. Область определения: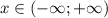
2. МНожество значений: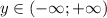
3. Найдем точки экстремума:
Находим производную:
Приравниваем ее к нулю:
Найденные точки разбивают область определения на три интервала:
Найдем знаки производной в этих интервалах, подставив значения из них (-2; 0; 2):
+ - +
Это значит, что функция на первом и последнем промежутках возрастает, а на среднем - убывает.
/ \ /
Найдем начения функции в этих точках:
1/3*(-1)^3-(-1)+3=-1/3+1+3=4-1/3=3+2/3=3,6666666
1/3*(1)^3-(1)+3=1/3-1+3=2+1/3=2+1/3=2,33333333
Т.о. функция вначале возрастает на промежутке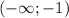 от
от 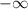 до
до 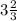 , после этого убывает на промежутке
, после этого убывает на промежутке 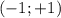 до
до 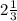 , и затем снова возрастает на промежутке
, и затем снова возрастает на промежутке 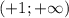 до
до 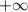
Осталось найти точки пересечения с осями координат:
ПРи х=0 у=3