x и y положительные действительные числа такие , что x + xy = 20y -y² и y +xy =21x - x² вычислите x + y

Ответы

7Оля8 18.01.2023 23:01

$\begin{cases} x+xy=20y-y^2 \\ y+xy=21x-x^2 \end{cases},\ x,y 0$

Сложим уравнения системы:

x+y+xy+xy=20y+21x-y^2-x^2

x+y+x^2+2xy+y^2=20y+20x+x

(x+y)+(x+y)^2=20(x+y)+x

$\boxed{(x+y)^2-19(x+y)=x}$

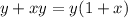Теперь умножим обе части первого уравнения на (y+xy) , причем в правой части вместо этого выражения запишем равное ему выражение (21x-x^2) . Поскольку y+xy=y(1+x) , то равняется нулю это выражение при неположительных значениях "х" и/или "у". Однако, по условию "х" и "у" - положительные числа, поэтому если при таком умножении и происходит потеря решений, то эти решения не удовлетворяют условию.

После умножения получим:

(x+xy)(y+xy)=(20y-y^2)(21x-x^2)

$x(1+y)\cdot y(1+x)=y(20-y)\cdot x(21-x)$

Поскольку по условию $x\neq 0;\ y\neq 0$ , то обе части равенства разделим на :

(1+y)(1+x)=(20-y)(21-x)

1+x+y+xy=420-20x-21y+xy

1+x+y=420-20x-21y

1+x+y=420-20x-20y-y

1+(x+y)=420-20(x+y)-y

(x+y)+20(x+y)+y=420-1

21(x+y)+y=419

Поменяем местами левую и правую части:

$\boxed{419=21(x+y)+y}$

Сложим левые и правые части равенств, записанных в рамках:

(x+y)^2-19(x+y)+419=x+21(x+y)+y

(x+y)^2-19(x+y)-21(x+y)-(x+y)+419=0

(x+y)^2-41(x+y)+419=0

Решаем квадратное уравнение относительно искомой суммы:

$D=(-41)^2-4\cdot1\cdot419=1681-1676=5$

$x+y=\dfrac{41\pm\sqrt{5} }{2}$

Как видно, два найденных значения суммы положительны. Вследствие этого нельзя гарантировать того, что для каждой из этих двух сумм "х" и "у" положительны.

Рассмотрим второе уравнение в рамке:

419=21(x+y)+y

y=419-21(x+y)

С этого уравнения мы сможем найти "у", а зная "у" и зная сумму - впоследствии найти "х". Таким образом, можно будет определить знаки чисел "х" и "у".

Выполним проверку для случая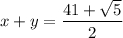 $x+y=\dfrac{41+\sqrt{5} }{2}$ :

$y=419-21\cdot \dfrac{41+\sqrt{5} }{2}=\dfrac{419\cdot2-21(41+\sqrt{5}) }{2}=$

$=\dfrac{838-861-21\sqrt{5} }{2}=\dfrac{-23-21\sqrt{5} }{2} < 0$

В этом случае значение "у" отрицательно. Значит, такой ответ не удовлетворяет условию.

Выполним проверку для случая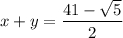 $x+y=\dfrac{41-\sqrt{5} }{2}$ :

$y=419-21\cdot \dfrac{41-\sqrt{5} }{2}=\dfrac{419\cdot2-21(41-\sqrt{5}) }{2}=$

$=\dfrac{838-861+21\sqrt{5} }{2}=\dfrac{-23+21\sqrt{5} }{2}$

Числитель оценим следующим образом:

$2=\sqrt{4} < \sqrt{5} < \sqrt{9} =3$

$42 < 21\sqrt{5} < 63$

$19 < 21\sqrt{5} -23 < 40$

Таким образом, числитель положителен. Значит:

$y=\dfrac{-23+21\sqrt{5} }{2} 0$

Найдем "х":

$x=(x+y)-y=\dfrac{41-\sqrt{5} }{2}-\dfrac{-23+21\sqrt{5} }{2}=$

$=\dfrac{41-\sqrt{5} +23-21\sqrt{5} }{2}=\dfrac{64-22\sqrt{5} }{2}=32-11\sqrt{5}$

Оценим следующим образом:

$2=\sqrt{4} < \sqrt{5} < \sqrt{6.25} =2.5$

$22 < 11\sqrt{5} < 27.5$

$4.5 < 32-11\sqrt{5} < 10$

Значит:

$x=32-11\sqrt{5} 0$

Таким образом, случай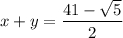 $x+y=\dfrac{41-\sqrt{5} }{2}$ удовлетворяет условию.

Решить систему можно было непосредственно выразив переменную "х" из первого уравнения и подставив полученное выражение во второе уравнение. Вся задача будет состоять только в аккуратном преобразовании, в результате которого должно получиться три значения "у": ноль, отрицательное и положительное. Поскольку по условию "у" должен быть положительным, то только для этого значения нужно будет просчитать значение "х", после чего найти требуемую сумму.

ответ: $\dfrac{41-\sqrt{5} }{2}$