X^4-3x^3+6x-4 =0 Как решать уравнения такого вида?
Другие вопросы по теме Алгебра
Популярные вопросы
- Реши . 1- й цех проиводит 15деталий в час. 2-й производит за 8-часовой...
1 - Найдите площадь круга , радиус которого равен 6 м. число п округи...
2 - Пассажирский поезд двигаясь со скоростью 90 км/ч за 3 часа проходит...
2 - Найдите площадь круга , радиус которого равен 6 м. число п округи...
2 - (2х+7)(х^2+12х-30)-5х^2=2х^2(х+1) ! не могу решить! не получается!...
3 - Через реку перенаправляется лодка, выдерживая курс перпендикулярно...
3 - Можно ли произведение корней из неотрицательных чисел заменить...
3 - Найди в тексте глаголы в сложной форме будущего времени.подчеркни...
3 - Оформи данные словосочетание,соблюдая правило.в каких случаях необходимо...
3 - Какая взаимосвязаны свобода и ответственность?...
1
1) Разложим на множители.
Сгруппируем:
2) Получаем два квадратных уравнения:
3) Решаем первое:
4) Решаем второе уравнение:
По теореме Виета получаем два корня:
ответ: {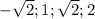 }
}
Старайтесь в таких уравнениях выполнить преобразования, чтобы получить квадратные уравнения, которые уже умеете решать.