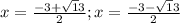X^4+2x^3-5x^2-2x+1=0 объясните, как решать
Другие вопросы по теме Алгебра
Популярные вопросы
- Укажите слово, в котором звуков больше чем букв. объятия, ученье,...
2 - Стороны прямоугольника относятся как 3 : 4 . найдите стороны прямоугольника...
3 - Какие основные тенденции развития в стране и в мире вы видите сегодня?...
2 - Вкаких случаях выполняется механическая работа...
2 - Какие последствия имела ликвидация казанского и астраханского ханств...
2 - Кмежвидовой борьбе за существование относится: 1) борьба за самку...
3 - Небольшой рассказ о том как труд меняет человека...
3 - Напиши все трехзначные числа в записи которых используется только...
1 - Состояние хозяйства собакевича. мёртвые души...
2 - Волк ужасно разъярён-съесть ежа не может он.(над каждым словом укажи...
1
Поделим исходное уравнение на x^2. Мы можем это сделать, так как при x=0 равенство не достигается.
Получаем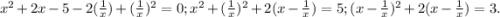
Сделаем замену. Пусть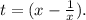
Тогда получим, что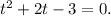
t=1 или t=-3.
Если t=1, то имеем: x^2-x-1=0.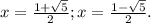
Если t=-3, то имеем: x^2+3x-1=0.