(x+3)^2+16=2|x+3|(|x-6|-|x-2)
решить)
Другие вопросы по теме Алгебра
Популярные вопросы
- «Быстрее. Выше. Сильнее. Чище» Прочитай текст «Спортсмен, принимающий допинг,...
2 - 360+65 қосындысы 13 ке бөліне ме...
1 - 4. Из предложенного перечня выберите два вещества, которые образуются при...
1 - розгляньте мал.15 структуру земельного фонду Європи. Порівняйте її зі структурою...
1 - Здание 2 Замените придаточные предложения причастными оборотами. Причастные...
1 - БЖБ АЛГЕБРА КОМЕКТЕСНДЕРШИ...
3 - Поняття, про яке йдеться у визначенні: «Сукупність усіх видів господарської...
1 - Ход белый королевий Лев киссиль О КОМ данный фрагмент?...
3 - Установи соответствие между рисунком и видом литосферного движения.коллизия...
2 - Мәтіннің негізгі айтар ойы неде? Клишеге сүйеніп екі сөйлеммен ой түйіндеңіз.Клише:Менің...
1
______|______|______|______
- 3 2 6
Объяснение:
Выделим в левой части полный квадрат. Для этого прибавим к обеим частям уравнения выражение и перенесем слагаемое
и перенесем слагаемое  в левую часть:
в левую часть:
1)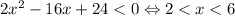
Тогда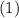 примет вид
примет вид
Левая часть неотрицательна. Правая часть, учитывая рассматриваемый интервал, строго отрицательна. Значит, корней на данном интервале нет.
2)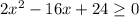
Возможны 2 случая:
2.1)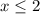
Тогда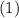 примет вид
примет вид
Оба корня принадлежат рассматриваемому интервалу, а значит являются корнями исходного уравнения.
2.2)
Тогда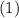 примет вид
примет вид
То есть корень не принадлежит рассматриваемому интервалу.