X^2-6x-7=0решити уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Read the text thean shoose what natural disaster each person below is speaking...
3 - 6. Решите уравнение: 3/5 |5х-3| + 2 - 11...
1 - Оқушылар екі сұрақтың (тақырыптың) біреуін таңдайды. Құрамы 100-150 сөзден тұратын...
1 - Следующее задание по истории, Расположите в хронологической последовательности...
1 - 1.б)Үлкен периодтарды көрсетіңіз А) 1,2,3 периодтар В) 1,2 период С) 4,5,6 периодтар...
2 - Представьте в виде рационального числа: -7/12; 5/7; -4/9; -121/144; 8/43; -2/3;...
1 - 2. Ерболдың ұсынысымен таныс. Қайта өңдеу«Қазіргі уақытта жер бетінде көптеген...
1 - Grammar 1 Look at the direct speech and complete the reported speech. ...
1 - Хто був майстром у створенні акоровіршів...
3 - На фотовыставке представлены фотографии российских и зарубежные фотографов, причем...
1
ответ на фото.........
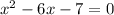
Найти:Значение квадратного уравнения.
Решение:для 8 класса (через дискриминант):
Вспоминаем вид уравнения, при котором можно вычислить дискриминант: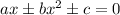 .
.
То есть наше уравнение , где
, где 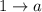 ,
, 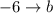 и
и 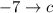 .
.
Вспоминаем формулу нахождения дискриминанта: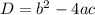 .
.
⇒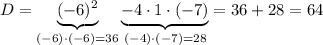
Вы (очень надеюсь) знаете, что есть правила дискриминанта:
Поскольку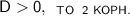
Вспоминаем формулу нахождения корней уравнения:
для 7 класса (через разложение трёхчлена):
Представим член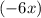 в виде выражения
в виде выражения 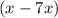 и запишем его в уравнение:
и запишем его в уравнение:
Произведение равно 0, если один из множителей равен 0.
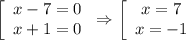
ответ: