((x-1)/4)-(2x-3)/2<(x²+3x)/8

Другие вопросы по теме Алгебра
Популярные вопросы
- Напиши, как ты понимаешь смысл словосочетания ложная тревога....
2 - Из яблок груш и абрикосов изготовили сок. груш в 3 раза больше чем абрикосов,...
2 - Написать небольшой отзыв о произведение гуливерн в стране лилипутов...
3 - Звучит так: методом электронного подберите коэффициенты в схемах окислительно-восстановительных...
2 - Одна сторона прямокутника а метрів , а друга у 9 разів більша . меншу...
3 - Золото - не дівка! окрім того, що красива,розумна,моторна і до всякого...
2 - С.яз а точнее с диктантом он не правильно написан . last sundry lines...
2 - Заряды 40 и -10 нкл расположены на расстоянии 10 см друг от друга. где...
3 - Обрубок дерева,короткобревно начинается на чу моейму брату сома не поняла...
1 - Подкиньте пару творческих идей . по участвую в семинаре, моя тема словари...
2
Объяснение:
(x-1)/4)-(2x-3)/2<(x²+3x)/8 - умножим на 8
2(x-1)-4(2x-3)<x²+3x
2х-2-8х+12<x²+3x
-6х+10<x²+3x
x²+3x>-6х+10
x²+9x-10>0
(x-1)(x+10)>0⇒ 1)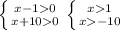 Отсюда (больше большего) х>1
Отсюда (больше большего) х>1
т.е х∈(1;+∞) либо
2)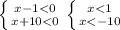 Отсюда(меньше меньшего) x<10 т.е.х∈(-∞;-10)
Отсюда(меньше меньшего) x<10 т.е.х∈(-∞;-10)
ответ: х∈(-∞;-10)∪(1;+∞)