1. Алгебра
  2. X ∈ [0;π], найти больший корень

X ∈ [0;π], найти больший корень уравнения 2cos(2x-π/3)=1

Anton222666222 Anton222666222    3   24.06.2021 19:03    0

Ответы
mauzeriss mauzeriss  24.07.2021 19:54

x=п

Объяснение:

\displaystyle 2cos(2x-\frac{\pi }{3})=1

\displaystyle 2*(cos(2x)*cos(\frac{\pi }{3})+sin(2x)*sin(\frac{\pi }{3}))=1

\displaystyle cos(2x)+\sqrt{3} sin(2x)=1

\displaystyle cos^{2}(x)-sin^{2}(x)+2\sqrt{3} sin(x)cos(x)=sin^{2}(x)+cos^{2}(x)

\displaystyle -2sin^{2}(x)+2\sqrt{3}sin(x)cos(x)=0

\displaystyle 2sin(x)*(-sin(x)+\sqrt{3}cos(x))=0

Произведение равно нулю, когда хотя бы один из множителей равен нулю

а)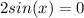 \displaystyle 2sin(x)=0

\displaystyle sin(x)=0

\displaystyle x=\pi n, n∈Z

б)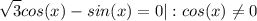  \displaystyle \sqrt{3} cos(x)-sin(x)=0| :cos(x)\neq 0

\displaystyle \sqrt{3}-tg(x)=0

\displaystyle tg(x)=\sqrt{3}

\displaystyle x=\frac{\pi}{3} +\pi n, n∈Z

Чтобы найти больший корень  нарисуем тригонометрическую окружность(см. вложение)

Из рисунка видно, что большим корнем на отрезке x ∈ [0;π] является x=п


X ∈ [0;π], найти больший корень уравнения 2cos(2x-π/3)=1
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
VasyaPupkin2281488 VasyaPupkin2281488  01.07.2019 07:10
В2008 году в городском квартале проживало 20000 человек. в 2009 году, в результате строительства новых домов, число жителей выросло на 4%, а в 2010 году — на 2% по сравнению...
пистолетМакарова пистолетМакарова  01.07.2019 07:10
Укажите число натуральных решений неравенства: | x/2-10 | = 3...
elenaelena6 elenaelena6  01.07.2019 07:10
Нужно решить вот это вот: y=2√x; x0=3 найти угол альфу вроде нужно, есть ещё такая строка |√х|^1= 1/2√x всё,...
Motia2k17 Motia2k17  01.07.2019 07:10
Изобразить график непрерывной функции : а) область определения функции ,есть промежуток [-4; 3] б) значение функции составляют промежуток [-1; 4] в) функция возрастает на...
25424446645 25424446645  01.07.2019 07:10
(x-5)(9x-1)/9-x o 9x=(1/27)^2-x log3(12-5x)=2 решите...
TanyaSha300 TanyaSha300  01.07.2019 07:10
Y=6x^8 - 3x^6 найти мин и мах, и точки экстремулы,+ рисунок! !...
adelya63Ada adelya63Ada  01.07.2019 07:10
Найдите значение производной функции f(x)=1+4х: 1+2х. в точках а) х=0 б) х=1...
Aigul1265 Aigul1265  01.07.2019 07:10
Y=6x(в 8 степени) - 3x(в 6 степени) найти мин и мах, и точки экстремулы,+ рисунок! !...
Kseniyagapchuk Kseniyagapchuk  01.07.2019 07:10
Sin 75 + sin 45 / cos 15 умоляю, решить нужно...
rid843 rid843  01.07.2019 07:10
Найти значение производной функции f(x)=3cos2x в точках а)х= пи: 4 б) х=0...

Популярные вопросы