Выясните при каких значениях x дробь х^4+7х^2+12/2х-х^2 положительна и при каких отрицательна.
Популярные вопросы
- СОР ПО МАТЕМАТИКЕ 6 КЛАСС 4 ЧЕТВЕРТЬ...
3 - Почему приборы магнитоэлектрической системы имеют равномерную шкалу?...
1 - Угол АВЕ развёрнутый, он разбит на три уголка (то есть, эти три угла...
1 - Задание 2. Перескажите кратко письменно сон, который приснился Светлане...
3 - Ex.1 – Выберите правильный вариант. 1) It sometimes (rains/ is raining)...
2 - Спишите предложения, расставьте знаки препинания. Обозначьте графически...
3 - Объясните сходства и различия между шведской и советской моделями социализма....
2 - 1 - тапсырма . Оқылым . Берілген өлеңдерді оқып , тапсырмаларды орындаңыз...
3 - Каким было верования оседлого населения? ...
3 - я сейчас умру ;-; у меня сор по естествознанию ...
3
Произведение двух положительных чисел положительно, значит, числитель дроби больше нуля при любых значениях переменной х. Тогда знак дроби зависит только от знаменателя.
2x - x² ≠ 0; x(2 - x) ≠ 0; x ≠ 0; x ≠ 2
Знаки многочлена 2x - x²
------------- (0) +++++++++ (2) ------------>x
1) x∈(-∞; 0) ∪ (2; +∞);
2x - x²< 0 ⇒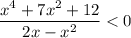
2) x∈(0; 2);
2x - x²> 0 ⇒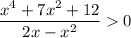
ответ: дробь положительна при x∈(0; 2);
дробь отрицательна при x∈(-∞; 0) ∪ (2; +∞).