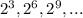Выяснить, является ли геометрической прогрессией последовательность, заданная формулой n-го члена: 1) bn = -5^2n; 2) bn = 2^3n;
Другие вопросы по теме Алгебра
Популярные вопросы
- Аюдын кыскы уйкыга кетуин кандай экологиялык факторга жаткызар...
1 - 1. Как Максат Рысдаулетов относится к своему поступку? Почему?...
2 - 4. Объясните на основе молекулярного строения вещества нагревание...
2 - Визначте масу 200 мл розчину натрій гідроксиду NaOH (густина розчину...
1 - Некоше(н,Hные, низкие кусты широко расстилались передо мною. (Тург.)Однажды,...
3 - Какие проблемные вопросы казахского края поднимали представители...
2 - Реши уравнение относительно х...
1 - Өнеркәсіптік мануфактуралық өндірістің таралуы...
3 - Докажите что в раннее средневековье папы римские обладали не только...
3 - В одном пачке 12 ручек. Сколько пачки ручек чтобы обеспечить 630...
3
да, обе
Объяснение:
1) -5²,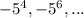
2)