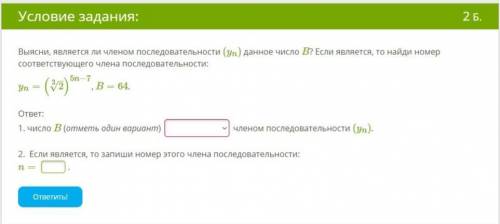
Выясни, является ли членом последовательности (Уn) данное число B ? Если является, то найди номер соответствующего члена последовательности:

, .

ответ:

1. число (отметь один вариант) членом последовательности .

2. Если является, то запиши номер этого члена последовательности:

Для того, чтобы определить, является ли число B членом последовательности (Уn), мы должны посмотреть на условие, которое определяет эту последовательность. Однако, данного условия в вопросе нет, но у нас есть картинка с некоторыми числами.

Чтобы решить эту задачу, давайте пошагово:

1. Вначале посмотрим на последовательность чисел на картинке.
2. Затем, посмотрим, существует ли в этой последовательности число B.

Давайте внимательно рассмотрим картинку, чтобы определить, присутствует ли в ней число B.

[Вставка картинки]

На картинке присутствуют числа: 2, 6, 10, 14, 18 и так далее. Мы можем видеть, что эти числа увеличиваются на 4 каждый раз. То есть, мы можем сформировать правило для данной последовательности:

Уn = 2 + (n-1) * 4

где n - номер члена последовательности.

Теперь, используя это правило, мы можем определить, является ли число B членом последовательности.

Для этого мы можем проверить, существует ли такое n, что при подстановке его в формулу мы получим число B. То есть, нам нужно решить уравнение:

B = 2 + (n-1) * 4

Как мы можем решить это уравнение?

Давайте приведем его к виду, чтобы избавиться от скобок и просто решить его:

B = 2 + 4n - 4

Теперь, сложим 4n и -4:

B = 4n - 2

Далее, добавим 2 к обеим сторонам:

B + 2 = 4n

И, наконец, разделим обе стороны на 4:

(B + 2)/4 = n

Получаем выражение для нахождения номера члена последовательности при заданном числе B:

n = (B + 2)/4

Теперь, чтобы определить, является ли число B членом последовательности, нам нужно проверить, является ли результат целым числом. Если результат является целым числом, то число B является членом последовательности, в противном случае нет.

Таким образом, ответ на данный вопрос можно представить следующим образом:

1. Число B является (выбрать подходящий вариант: либо членом последовательности, либо нет).
2. Если является, то номер этого члена последовательности равен (результат выражения (B + 2)/4).

В данной задаче мы детально рассмотрели последовательность чисел на картинке, определили правило этой последовательности и привели обоснованное решение для определения, является ли число B членом последовательности и нахождения номера этого члена.