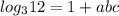Выразите log3(12 ) через a, b, и c, если log3(7)=a, log7(5)=b, log5(4)=c
Другие вопросы по теме Алгебра
Популярные вопросы
- При каком натуральном значении X равенство будет верным ...
1 - . Енергія випромінювання, поглинена тілом, — 100 Дж. Чому дорівнює доза поглиненого...
3 - Как зависит сопротивление полупроводников от температуры ?...
2 - Напишите 3притяжательных местоимен, 3 личных местоимен, составьте с ними 4 предлажения...
3 - и подпишусь умаляю я в этом нуждаюсь...
2 - 16. Прочитайте предложения и определите, в каких словах Незнайка допустил ошибку.Лодка...
1 - Цистинурия - заболевание почек, связанное с нарушением реабсорбции цистина....
2 - Тело массой m= 2кг движется прямолинейно по закону х(t)=(5t+1)2 (м). Найдите...
1 - Билеушілер Саяси іс-әрекеттер1. Тоғылық Темір2. Қызыр ҚожаА) Әмір Темір бодандығын...
1 - НУЖНО РЕШИТЬ УРАВНЕНИЕ 0,123х = 123...
2
Решение.
1) Каждый из данных логарифмов выразим через десятичные логарифмы
2) Найдем произведение.
3) Находим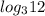
ответ: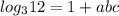
1)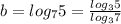
2)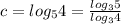
3)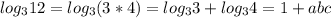
ответ: