Выражения
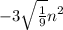
$- 3 \sqrt{ \frac{1}{9} } n {}^{2}$
если n < 0

Ответы

sokolovvw1 26.01.2024 13:42

Для решения данной задачи, нам необходимо выразить данное выражение. Для начала, рассмотрим известные нам математические правила.

1. Квадратный корень из числа $\sqrt{a}$ представляет собой число, при возведении в квадрат которого получится число "a". Например, $\sqrt{9} = 3$ , так как $3^2 = 9$ .

2. Умножение чисел на отрицательное число меняет знак результата. Например, $-2 * 3 = -6$ .

Теперь решим данное выражение:

$- 3 \sqrt{ \frac{1}{9} } n {}^{2}$

Раскроем скобки и упростим выражение:

$- 3 * \frac{1}{3} * n {}^{2}$

Сократим дробь:

$- 1 * n {}^{2}$

Далее, применим правило умножения чисел на отрицательное число:

$- n {}^{2}$

Известно, что $n$ - отрицательное число, поэтому возведем его в квадрат:

$- (-n) * (-n)$
$n * n$
$n {}^{2}$

Таким образом, ответ на данное выражение будет $n {}^{2}$ .

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра