Выражения: (объясните дубу-как это делается? ) с^2+4c+4 а) : (c+2) c^2-4 б) (x-2)(x+4)-2x(1+x) (2a a-b ) в) + * b (a-b b ) ( 1 1 ) 2ab г) + * ( a b ) a^2-b^2
Другие вопросы по теме Алгебра
Популярные вопросы
- 8класс 2 1. из перечня веществ и смесей выберите простые вещества, сложные...
1 - Напишите рассказ ,,волшебная сказка из 7-9 предложений...
1 - Составьте экскурсию 6 класс по архитектурным памятникам византии...
1 - Плохо сокращаю дроби. нужно обьяснить как сокращать...
3 - Православная церковь причислила первую княгиню -христианку к лику...
2 - Найдите значение выражения: (0,8+6,5)(7,2-13,2)...
2 - Являются ли минеральные вещества фактороми среды для ростений ( ответ поясните)...
1 - 81. прочитайте. составьте словосочетания, подбирая к главному слову зависимое...
3 - Обозначьте грамматическую основу : вашингтон-столица сша. париж-столица франции.лондон-столица...
3 - Составьте рассказ о занятиях древнейших людей...
3
с^2+4c+4
а) ---------- : (c+2)
c^2-4
с^2+4c+4 можно свернуть по формуле:с^2+4c+4=(с+2)^2
c^2-4 можно расписать по формуле:c^2-4=(с+2)(с-2)
Получается:
(с+2)^2
---------- :(c+2)
(с+2)(с-2)
Сокращается и остается:
(с+2)
------:(c+2)
(с-2)
Дальше, сокращаем (с+2) и остается:
1
----
(с-2) решено:))
б) (x-2)(x+4)-2x(1+x)
Перемножаем 2 скобки, получается: x^2+4x-2x-8
далее раскрываем 3ю скобку:-2х-2х^2
получается:x^2+4x-2x-8-2х-2х^2
приводим подобные:
-х^2-8=0
х^2=-8
x=+-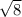
(2a a-b )
в) ------ + ------ * b
(a-b b )
работаем со скобками, приводим к общему знаменателю:
(2аb+(a-b)^2)
----------------- *b
b(a-b)
раскрываем скобки в числителе: 2ab+a^2-2ab+b^2
приводим подобные:a^2+b^2=(a-b)(a+b)
Итак:
(a-b)(a+b)
------------ *b
b(a-b)
сокращаем и получается: a+b
( 1 1 ) 2ab
г) ---- + --- * ---------
( a b ) a^2-b^2
В скобках приведем к общему знаменателю:
a+b 2ab
---- * -----
ab a^2-b^2
a^2-b^2 можно свернуть по формуле:a^2-b^2=(a-b)(a+b)
a+b 2ab
---- * -----
ab (a-b)(a+b)
Сокращаем, получается:
2
----
a-b
с^2+4c+4
а) : (c+2)=
c^2-4
(с+2)^2
:(c+2)=
(с+2)(с-2)
(с+2)
:(c+2)=
(с-2)
1
(с-2)
б) (x-2)(x+4)-2x(1+x)= x^2+4x-2x-8=x^2+4x-2x-8-2х-2х^2
-х^2-8=0
х^2=-8
x=+-корень из восьми
(2a a-b )
в) + * b=
(a-b b )
(2аb+(a-b)^2)
*b=
b(a-b)
(a-b)(a+b)
*b=
b(a-b)
=a+b
( 1 1 ) 2ab
г) + --- * =
( a b ) a^2-b^2
a+b 2ab
* =
ab a^2-b^2
a+b 2ab
* =
ab (a-b)(a+b)
2
a-b