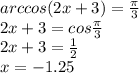Выражения: 1. sin ( pi/4 + alpha ) - sin (pi/4 - alpha ) 2. sin ( pi/6 + alpha ) +sin (pi/6 - alpha ) решить уравнения: 1. arcsin (2-3x) = pi/6 2. arccos (2x+3) = pi/3
Другие вопросы по теме Алгебра
Популярные вопросы
- Проблемы, связанные с личностью, которые не являются прерогативой...
3 - Социальную перцепцию определяют как … процесс, включающий в себя...
3 - Поддерживая в рамках благотворительных программ социально незащищенные...
3 - В США содержание понятия «деловая этика» … подразумевает ответ...
3 - Страны, в которых стала формироваться концепция социально ответственного...
1 - Подход к изучению корпоративной социальной ответственности, который...
2 - Две основные экономические составляющие маркетинговой концепции...
3 - Причина упразднения и существенного урезания программ социальной...
2 - Общая черта в трактовке понятия «деловая этика» в США и Европе...
2 - Конкурентное преимущество, которое обеспечивает компании в странах...
3
Упростим:
1.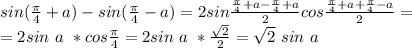
2.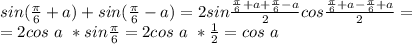
Уравнения:
1.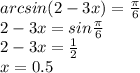
2.