Выражение
(у в квадрате / х^3 - ху^2 + 1/х+у) : (х-у/х^2 +х у - х/ху+ у^2

Объяснение:

Расставим порядок действий:

Первое и второе действие в скобках, третье - деление.

Решаем первое действие.

Для начала вспомним, что для того, чтобы вычесть или сложить алгебраические дроби, необходимо знаменатели дробей разложить на множители и привести их к общему знаменателю.

В знаменателе первой дроби мы можем вынести за скобку x.

Получим:

В знаменателе первой дроби у нас появилась формула разности квадратов. Развернем эту формулу и получим:

Теперь мы можем смело привести эти дроби к общему знаменателю.

Во второй дроби есть x + y, давайте-ка домножим вторую дробь на те  множители, которые есть только у первой дроби, т.е., на x и на (x - y)

Имеем:

Справка: мы домножили на множители и числитель, и знаменатель.

Раскроем скобки во второй дроби и сложим числители дробей:

Второе действие:

Делаешь все то же самое. ответ ко второму действию: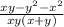 или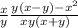

Третье действие: