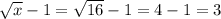Выражение и найдите его значение
буду любой )
![(1 + 2\sqrt[4]{x} + \frac{x - \sqrt{x} }{\sqrt{x} - 1 }) * \frac{x^{\frac{1}{4} } -1 }{x^{\frac{1}{4} } +1 }](/tex.php?f=(1 + 2\sqrt[4]{x} + \frac{x - \sqrt{x} }{\sqrt{x} - 1 }) * \frac{x^{\frac{1}{4} } -1 }{x^{\frac{1}{4} } +1 })
при x=16
Другие вопросы по теме Алгебра
Популярные вопросы
- В каком году началась и закончилась первая мировая? В каком году началась и закончилась...
1 - Какой герой больше всего понравился в рассказе И.С.Тургенева ,,Бежин луг,, И почему...
1 - Как Вы понимаете значение слова ОСТОРОЖНОСТЬ? Сформулируйте и прокомментируйте данное...
3 - 1+100-37+2839+500-607+347-600...
3 - Когда и как зародилось искусство...
1 - Вариант 2 01. Выбери верный порядок выполнения сло- жения в столбик. 1) Записать...
1 - 1. Составьте хронику событий лета 1914 г., приведших к началу Первой мировой войны....
3 - Точка M — середина стороны BC параллелограмма ABCD. Выразите вектор AM через векторы...
2 - Головни та другорядни герои Гарри Поттер и философский камень ...
2 - Нулевая степень означает, что число должно само на себя поделиться. 0^0 = 0/0. Деление...
1
решение представлено на фото
Если х = 16, то