Вычислите значение дроби 4a+9b/5a-b, если 3a+5b=0
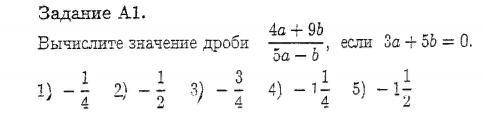
Другие вопросы по теме Алгебра
Популярные вопросы
- #1. у грибов отсутствует к фотосинтезу , так как : а)они имеют небольшие...
2 - Кошка +кошка+кошка =собака какие буквы такие и цифры...
2 - Составить предложение со словом столетний дуб...
2 - Написать сочинение на тему любимец можете написать про рыбку или про собаку...
3 - Северная ширина и западная долгота озера эйр нот и якутска и сантьяго...
3 - Начертите отрезок ма 6 см. начертите отрезок ав , длина которого составляет...
1 - Точка с запятой ; почему его ставят...
3 - Какие действия гормонов ожидается,когда человек нуждается в энергии? а.увеличение...
3 - Расположите числа в порядке возрастания: корень 2,3, корень 10,4, корень...
2 - 1. є 900 г кухарської солі, дві посудини, терези та гирі масою 5 г і 20...
3
(4а+9b)/(5a-b) = (3a+5b+a+4b)/(5a-b)
Если 3а+5b=0, (3a+5b+a+4b)/(5a-b) = (a+4b)/(5a-b)
3a = -5b, поэтому (a+4b)/(5a-b) = (-1,67b+4b)/(-8,33b-b) = 2,33b/(-9,33b) = -0,25 или - 1/4
Відповідь:
Пояснення: