Вычислите tg^4 x + ctg^4 x, если tgx+ctg=5
Ответы
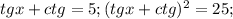
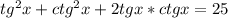 (испоьзуем свойство
(испоьзуем свойство 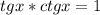 )
)
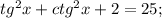
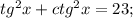
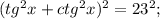
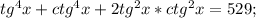
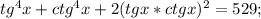
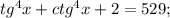
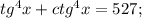
Другие вопросы по теме Алгебра
Популярные вопросы
- Составить уравнение плоскости проходящую через точку M(1,0,1) перпендикулярно...
3 - Это не помешало мне с увлечением прочесть два первых томика, но перечесть их...
3 - прачытыйце сказы, пастауце, дзе трэба, знаки прыпынку. Падкрэслице граматычныя...
2 - Хто автор цього зошита і як він називається?...
3 - Лампа А розташована в коридорі перед відкритими дверими до кімнати.Покажіть...
3 - Анаэробный этап представляет собой процесс бескислородного расщепления молекулы...
1 - Задание 12. Представьте себе, что вы - руководитель крупной туристской фирмы....
1 - А) Неорганические вещества, содержащие несколько элементов – это …………………………………………………………………………………...
1 - Дана окружность х2 – 10х + у2 + 2у + 17 = 0. Напишите уравнение образа этой...
1 - Выберите функции, графики которых параллельны, пересекаются и совпадают, ответ...
3