Вычислите производную f'(п/9) , если f (x)=lncos3x
Другие вопросы по теме Алгебра
Популярные вопросы
- Вроссии идет процесс формирования гражданского общества. примеры(3 примера)...
2 - Марьям потратила на приготовление 45минут,а айбек -на 5 раз меньше.на сколько...
1 - Для чего автор использует олицетворение?...
2 - Решите выберите схемы не осуществимых реакций 1)naoh+hcl= 2) nacl+kno3= 3)...
3 - Как великий шелковый путь повлиял на развитие напишите ответы...
3 - Решить найдите множество корней уравнения (x^2-1) (x^2+5x+6)=0...
3 - К80 г раствора с массовой долей соли 0.75 прибавлено воды 25г определите...
2 - Примеры из жизни связанная с правом с социальной сферы общества...
2 - Как великий шелковый путь повлиял на развитие строительства...
2 - Выражение: 14х-3х+х 16у+125+14у+9 25×m×16...
2
f'(x)=ln(cos3x)=(3x)'*(cos3x)'*(lncos3x)'=3*(-sin3x)*(1/cos3x)=-3sin3x/cos3x=-3tg3x
при х=п/9, f'(x)=f'(п/9)=-3(tg(п/3))=-3*корень квадратный из 3
f'(x)=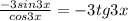
f'(П/9)=-3*tgП/3=-3√3