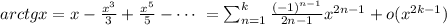Вычислите предел

(без использования правила лопиталя)
Другие вопросы по теме Алгебра
Популярные вопросы
- Перевести текст, . international students the university of oxford is home...
3 - Какова будет массовая доля хлорида калия в растворе если три моря её растворили...
2 - 2. укажіть рівняння ендотермічної реакції: а) 2kcio, - 2kcl + 30); ah =...
2 - Прискорення тіла = 3 м/с за 5 хв швидкість тіла змінилась до 100 м/с. визначити...
2 - Контрольный тест. определить тип придаточных определить тип придаточного...
2 - We all like our swimming pool.and many children (пропущено) there every...
3 - Визначте формулу алкіну відносна молекулярна маса якого 54 будь ласка...
1 - Рівняння реакції метанової кислоти з а)карбонатом кальцію б)оксидом магнію...
3 - 50 ! very ! нужны 3,4,5 желательно выполненые на листке) за эт отдельный...
1 - 15 ! тестик по « песнь о вещем олеге » (не смотрите на то что я сделала...
3
Использовано разложение в ряд Тейлора