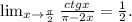ВЫЧИСЛИТЕ ПРЕДЕЛ, С РЕШЕНИЕМ
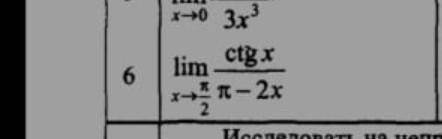
Другие вопросы по теме Алгебра
Популярные вопросы
- 1.,связанные с многолетней мерзлотой....
2 - Имена героев в рассказе чехова толстый и тонкий...
3 - Вкаких произаедениях, помимо пушкина медный всадник , представлен конфликт обычного...
2 - Треугольник абс прямоугольный угол с равен 90 , а равен 60, cx высота абс, причём...
1 - 1. в коробку положили 15 конфет маска , 20 конфет ромашка и 40 ирисок. какую...
3 - 6(2x+1/6)=5(2,24x+0,2) линейное уровнение с одной переменой)...
3 - Преобразуйте выражения используя формулы сокращенного умножения (x+y)2 4x2+12x+9...
1 - Определите объём аммиака, полученного при взаимодействии 6 моль водорода с 3...
2 - 1) растения семейства бобовые богаты белками, так как они а. развиваются из...
1 - Назовите 2 изменения климата, вызванные созданием водохранилища.!...
1
Объяснение:
Применяем 1-е правило Лопиталя:
ответ: