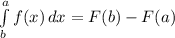Вычислите площадь фигуры, ограниченной заданными линиями. y=7x-x^2; y=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Известно, что информация о последовательности аминокислот в белках содержится...
3 - Мастером стихотворной сказки был: 1)э.успенский 2)н.носов 3)а.пушкин 4)и.крылов...
1 - Fecl2 + x = y + nacl сколько будет?...
2 - Как удается писателю в.каверину с первых страниц романа два капитана создать...
3 - Найдите примеры в литре настоящую дружбу...
2 - Акой отряд млекопитающих самый малочисленный и находится под угрозой вымирания?...
3 - Белый кролик (аа) скрещивается с черным кроликом (аа).гибридные кролики...
2 - Вклумбе посажено 1/6 роз,остальные 3/5 гвоздик,остальные 120 штук другие...
2 - Из точки, не лежащей в некоторой плоскости, построены два отрезка длиной...
3 - Что сближает павла петровича с базаровым в их словестных поединках и судьбе?...
2
343/6≈51.167
Объяснение:
Начертим график для параболы. Из него видно, что она располагается в пределах от 0 до 7 . В этих пределах мы и будем интегрировать функцию.
Подставляем пределы по формуле Ньютона-Лейбница: