Вычислите определённый интеграл от 0 до Пи sin² x dx.
Другие вопросы по теме Алгебра
Популярные вопросы
- Жуковский светлана .вопрос: какой « толк» дает автор? что является,...
1 - Какие книги нужно обязательно прочитать?...
1 - Как сделать шаблон параболы? я его начертила на картонке, что дальше?...
3 - Впрямоугольной комнате следует расставить 10 стульев так,чтобы у кождой...
2 - Составить предложение которое побуждает кого либо тема написать о...
3 - Составь сложные по составу и смыслу слова из таких слов: 1) добро...
3 - Характеристика согласных и гласных букв...
3 - Решите уравнение напишите решение (6x-d)*8=104при d=29...
3 - Как вычислить в обратном направлении ? -17+9×9÷2÷6×9=45...
2 - Че такой не можно еще другой вариант...
2
π/2
Объяснение:
sin²x=(1-cos2x)/2=½(1-cos2x) - формула понижения степени
Применяем формулу понижения степени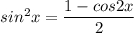 .
.