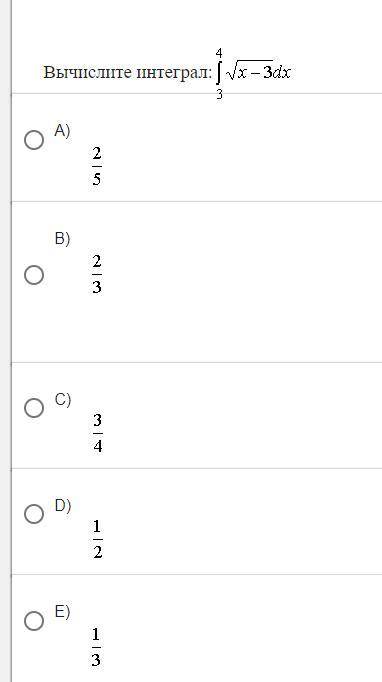
Вычислите интеграл вычислите интеграл
Другие вопросы по теме Алгебра
Популярные вопросы
- Каких знаменитых путешественников вы знаете ? напишите об одном из...
2 - Значения двух массивов a[1..100] и b[1..100] с следующего фрагмента...
3 - Прочитай скороговорки вспомни зачем они нужны спиши вставь пропущенные...
3 - Ккаждому примеру подберите и запишите по два однокаренных слова с...
2 - Сочинение на тему любовь к братьям нашим меньшим...
3 - Разбор по составу книги книголюб книгопечатание книгоиздательство...
1 - Напиши ответы на вопросы,используя слова лиса. укажи падеже имени...
2 - Составить программу вычисления х2 – 2, если х либо = 4 у = х2 – 2х...
2 - Отличается ли синтаксис от синтаксических норм? надо!...
1 - Речення зі словом не продумавши ! проводите !...
3
Объяснение:
ответ В
Вычислите интеграл:
1. Представим квадратный корень в виде степени с рациональным показателем:
2. Для функции вида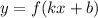 интеграл находится следующим образом:
интеграл находится следующим образом:
где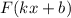 ― одна из первообразных функции
― одна из первообразных функции 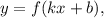
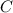 ― произвольная постоянная.
― произвольная постоянная.
Таким образом, воспользуемся нахождением интеграла степенной функции:
Имеем:
3. Воспользуемся формулой Ньютона-Лейбница:
Имеем:
ответ: