Вычислите интеграл Варианты ответов
1) (π - 8) / 32
2) (3π - 4) / 32
3) (3π - 8) / 32
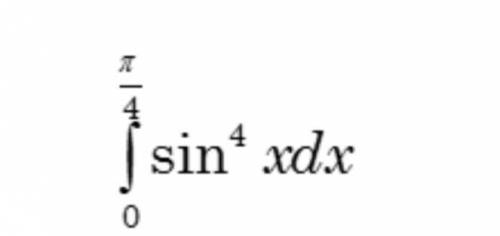
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычислите во сколько раз октан тяжелее водорода...
1 - Какие существуют установления порядка в обществе? какие существуют...
3 - 1-4 5+3 б из одного села одновременно в противоположных направлениях...
1 - Закончите уравнения реакций протекающих с образованием воды, напишите...
3 - Формула сильного электролита: 1)hci 2)baso3 3)caco3 4)mg(oh)2 в ряду...
1 - Решить ! два одинаковых насоса выкачивают из подвала воду: первый...
1 - Для перевозки молока созданы специальные -гиганты. в году город обслуживали...
1 - Придумать предложение со словом навзничь...
2 - Теория вероятностей используя правило сложения вероятностей, вычислите...
2 - Расставить скобки 30-1-1+2=32, 90+50-40-10=90...
3
ответ: №3 .