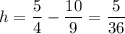Вычислите интеграл :

Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите уравнения реакций,позволяющих осуществить следующие...
1 - Нужно заранее .b)britain 1.when did england become a great country?...
2 - Разобрать 2 слово по составу- грянул и пришёл...
3 - H2c-c(ch3)-ch2-ch(c3h7)-ch3 -как называется?...
3 - Решить подробно ( надо): sin 240 градусов - cos 400 градусов...
1 - Собственная скорость катера 18 км/ч скорость течения реки 2 км...
1 - Водной коробке носки голубые , а в другой белые. голубых на 20...
2 - образования летчик , парашютистка , электровоз . малодоступный...
3 - При совместной работе двух тракторов после было вспахано за 20...
2 - Заполните пропуски в высказывании: гражданин должен платить с...
3
Стандартными решить интеграл никак, но графически можно найти площадь фигуры, ограниченными линиями x = 5/4 и x = 10/9. Из школьного курса мы делали полное исследование функции. Не составит труда Вам это вспомнить и построить график.
Найдем точки пересечения графика функции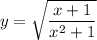 с прямыми x = 5/4 и x = 10/9
с прямыми x = 5/4 и x = 10/9
Вот и на рисунку есть примерный график. Похож на прямоугольную трапецию и не трудно найти ее площадь. Высота трапеции: