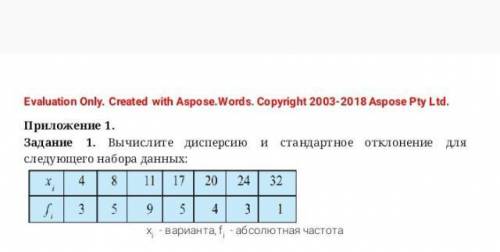
Вычислите дисперсию и стандартное отклонение для следующего набора данных:
♥️​

Для вычисления дисперсии и стандартного отклонения нам необходимо выполнить несколько шагов.

Шаг 1: Найти среднее значение сердечек в данном наборе данных.
Суммируем все значения сердечек: 5 + 4 + 6 + 6 + 3 + 2 = 26.
Делим сумму на количество значений: 26 / 6 = 4.33.
Среднее значение сердечек равно 4.33.

Шаг 2: Вычислить отклонение каждого значения сердечек от среднего.
Отклонение для каждого значения равно значение - среднее значение.
Для первого значения 5 - 4.33 = 0.67.
Для второго значения 4 - 4.33 = -0.33.
Для третьего значения 6 - 4.33 = 1.67.
Для четвертого значения 6 - 4.33 = 1.67.
Для пятого значения 3 - 4.33 = -1.33.
Для шестого значения 2 - 4.33 = -2.33.

Шаг 3: Возвести каждое отклонение в квадрат.
Для первого значения 0.67^2 = 0.4489.
Для второго значения -0.33^2 = 0.1089.
Для третьего значения 1.67^2 = 2.7889.
Для четвертого значения 1.67^2 = 2.7889.
Для пятого значения -1.33^2 = 1.7689.
Для шестого значения -2.33^2 = 5.4089.

Шаг 4: Найти сумму квадратов отклонений.
Суммируем все значения из предыдущего шага: 0.4489 + 0.1089 + 2.7889 + 2.7889 + 1.7689 + 5.4089 = 13.3145.
Сумма квадратов отклонений равна 13.3145.

Шаг 5: Вычислить дисперсию.
Дисперсия равна сумме квадратов отклонений, деленной на количество значений.
Для данного набора данных: 13.3145 / 6 = 2.22.
Дисперсия равна 2.22.

Шаг 6: Вычислить стандартное отклонение.
Стандартное отклонение является квадратным корнем из дисперсии.
Квадратный корень из 2.22 ≈ 1.49.
Стандартное отклонение равно 1.49.

Итак, дисперсия для данного набора данных равна 2.22, а стандартное отклонение равно 1.49.
Эти значения показывают, насколько значения сердечек в наборе данных отклоняются от их среднего значения.